有理数和无理数的定义

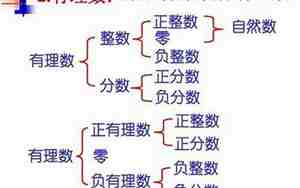
有理数和无理数的定义：

有理数是指可以表示为两个整数比的数，即它们可以写成分数形式 \( \frac{p}{q} \)，其中 \( p \) 和 \( q \) 是整数，且 \( q \) 不为零。这些数的运算可以精确进行，因为它们可以被表示为有限或无限循环的小数形式，如 \( \frac{1}{2} = 0.5 \)，\( \frac{3}{7} = 0.\overline{428571} \)。

无理数则与有理数相反，它不能被写成两个整数的比。无理数的小数部分既不是有限的也不是循环的，也就是说，它们不能简化为分数形式。例如，圆周率 \( \pi \) 和自然对数 \( \ln(2) \) 都是无理数，因为它们的小数部分是无限且不重复的，如 \( \pi = 3.14159... \)。

分类：

1. 整数（\( Z \)），包括正整数、负整数和零，是有限元，有理数的一部分。
2. 分数（\( Q \)），即两个整数的比，形成有理数数集。
3. 有理数（\( \mathbb{Q} \)），包括整数和所有可以表示为分数形式的数，是有理数集，它是实数集 \( \mathbb{R} \) 的子集。
4. 无理数（\( \mathbb{R} \backslash \mathbb{Q} \)），是实数集中的那些不能表示为有理数的数，它们构成了实数集的一个无限且密集部分。

无理数的性质使得它们在几何和数学分析中起到了关键作用，例如，无理数的长度可以是无法用两个有理数比精确测量的，如黄金分割比例 \( \phi \) 就是一个著名的无理数。

有理数和无理数的定义区别在哪里

有理数和无理数的定义区别主要在于它们的表示形式及小数表示的特性：

有理数的定义：

有理数是可以表示为两个整数的比率的数，即 \( \frac{p}{q} \)，其中 \( p \) 和 \( q \) 是整数，且 \( q \) 不等于零。它们可以写成有限的、无限循环的，或者是可以简化为最简分数的形式。例如，\( \frac{1}{2} = 0.5 \)，\( \frac{10}{3} = 3.\overline{3} \)。

无理数的定义：

无理数无法表示为两个整数的比率，它们的小数部分既不是有限的，也不是无限循环的，且不能简化为分数形式。例如，圆周率 \( \pi \) 和自然对数 \( \ln(2) \) 就是无理数，它们的值是 \( 3.14159... \) 和 \( 0.693147... \)，小数点后的数字是无限且没有重复模式。

区别

1. 表现形式：有理数可以写成分数形式，可以转换为有限小数或无限循环小数；无理数不能写成分数形式，小数部分是无限且非循环的。
2. 分类：有理数是一类，包括整数和分数；无理数是另一类，是实数集中的一个无限子集。
3. 运算：有理数的加、减、乘、除运算结果仍为有理数；无理数的这些运算法则下，结果可能为有理数（如 \( \sqrt{2} \times \sqrt{2} = 2 \) 为有理数）或无理数（如 \( \pi + \pi \) 为无理数）。

有理数和无理数是实数的基本分类，它们共同构成了实数集。